촘스키 계층구조Chomsky Hierarchy

촘스키 계층구조Chomsky  Hierarchy

 

......... 언어는 그 언어를 생성하는 최대로 제한되는 문법의 정도에 따라 구분한다.이는 촘스키 계층 (Chomsky hierachy) 이라고 하는, 제한된 문법의 형태 (따라서 각 문법에 의하여 생성되는 언어도 제한됨) 를 정의하는 한 가지 방법이다 .............

촘스키 계층 (Chomsky hierachy) 는 형식언어 (Formal Language) 를 생성하는 형식문법 (Formal Grammar) 들을 분류해 놓은 계층구조이다. 1956 년에 Noam Chomsky 가 처음 서술하였다. 그 계층구조는 다음과 같이 구분한다.

• Type-0 문법 (unrestricted grammars) 은 모든 형식문법을 포함한다. 튜링기계 (Turing Machine) 로 인식가능한 모든 언어를 정확히 생성한다. 그 인식가능한 언어란 튜링기계가 멈추는 모든 string 들을 의미한다. 이 언어들은 또한 회귀열거가능 언어 (recursively enumerable languages) 로 알려져있다. 이것은 튜링기계를 항상 정지시켜서 결정가능한 (decided)  recursive language 와는 다르다는 것을 주목해야 한다.

• Type-1 문법 (context-sensitive grammars) 은 context-sensitive languages 를 생성한다. 이 문법은 αAβ → αγβ 형태의 규칙을 가진다 (A a nonterminal and α, β and γ strings of terminals and nonterminals), strings α 와 β 는 empty 일 수 있지만 γ 는 nonempty 이어야 한다. 만일 S 가 어떤 규칙의 우측에 나타나지 않으면 규칙 S → ε 가 허용된다. 이 문법으로 묘사되는 언어는 non-deterministic Turing machine (테이프가 입력의 길이를 constant time 으로 제한된) 으로 인식가능한 모든 언어들이다.

• Type-2 문법 (context-free grammars) 은 context-free languages 를 생성한다. 이것은 A → γ 의 형태를 가지는 규칙으로 정의된다 (A a nonterminal and γ a string of terminals and nonterminals). 이 언어들은 non-deterministic pushdown automaton 로 인식가능한 모든 언어들이다. Context free languages 는 대부분의 프로그래밍 언어 문법의 이론적 기초이다.

• Type-3 문법 (regular grammars) 은 regular languages 를 생성한다. 여기서는 왼쪽에 단 하나의 nonterminal 과 오른쪽에 단 하나의 terminal을 가지고, 단 하나의 nonterminal 이 뒤따르도록, 규칙을 제한한다. 만일 S 가 규칙의 오른쪽에 나타나지 않으면 규칙 S → ε 이 허용된다. 이 언어들은 finite state automaton 으로 결정가능한 모든 언어들이다. 덧붙여서 이러한 부류의 형식언어들은 regular expressions 으로 얻어질 수 있다. Regular languages 는 search patterns 과 프로그래밍 언어의 어휘구조를 정의하는데 흔히 사용된다.

4 가지 유형의 문법, 그 문법이 생성하는 언어의 종류, 그 문법을 인식하는 오토마톤의 유형, 그 문법규칙들이 가지는 형태 .............. (Wikipedia : Chomsky hierarchy)

Grammar	Languages	Automaton	Production rules
Type-0	Recursively enumerable	튜링기계 (Turing Machine)	No restrictions (제한없음)
Type-1	Context-sensitive	Linear-bounded non-deterministic Turing machine	αAβ → αγβ
Type-2	Context-free	Non-deterministic pushdown automaton	A → γ
Type-3	Regular	Finite state automaton	A → aB A → Ba A → a

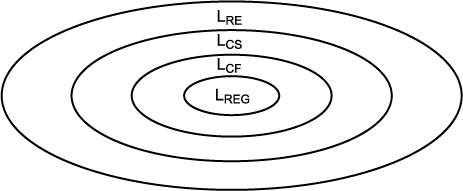
......... 지금까지 여러 가지 언어군들을 살펴보았다. 순환적으로 열거가능한 언어 , 문맥-인식 언어 , 문맥-자유 언어 , 정규 언어  등이 여기에 해당한다. 이 언어군들 사이의 관계를 나타내는 한 가지 방법이 Chomsky 계층이다. 형식 언어 이론의 창시자인 Noam Chomsky 는 초기에 언어들을 네 가지 언어 형식들, type 0, type 1, type 2, type 3 으로 분류하였다. 이 원래의 용어가 지속되어 왔고, 사람들이 그것을 자주 참조하지만, 번호로 매겨진 형식은 실제로 우리가 연구하였던 언어군들에 대한 다른 이름들이다. type 0 언어는 무제한 문법에 의하여 생성되는 언어들이다. 즉, 순환적으로 열거가능한 언어이다. type 1 은 문맥-인식 언어들로 구성되고, type 2 는 문맥-자유 언어들로 구성되며, type 3 은 정규 언어들로 구성된다. 우리가 살펴본 바와 같이 type i 의 각 언어군은 type i - 1 언어군의 진부분 집합이다. 그림 3 의 다이어그램은 이들 사이의 관계를 명확히 보여준다. 그림 3 이 원래의 Chomsky 계층을 보여준다................. (Peter Linz 2001)

다음 표에서는 계산가능성 이론 (Computability Theory) (청색) 과 계산복잡도이론 (Computational Complexity Theory) (녹색) 에서 고려되는 문제들 (또는 언어, 문법들) 을 분류하는 일부를 보여준다. 만일 문제 X 가 Y 의 진부분집합 이라면 X 는 Y 의 아래에 위치하고 검은색 선으로 연결된다. 만일 X 가 부분집합이지만 같은 집합 (equal sets) 인지도 모를 때는 점선으로 연결된다.  

		Decision Problem
Type 0 (Recursively enumerable)				Undecidable
Decidable
EXPSPACE
EXPTIME
PSPACE
Type 1 (Context-sensitive)							PSPACE-Complete
		Co-NP			NP
			BPP		BQP		NP-complete
		P
	NC						P-Complete
Type 2 (Context-free)
Type 3 (Regular)

term :